위상정렬 indegree 방법

indegree란 한 정점에서 자신에게 들어오는 방향인 간선의 수입니다.

 

다음과 같은 그래프에서 각정점의 indegree의 개수는

 

1번 정점: 0

2번 정점: 1

3번 정점: 0

4번 정점: 3 

 

이 됩니다. 즉 화살표 방향이 자기를 향하고 있는 간선의 개수 입니다.

 

우리는 간선의 정보를 받을 때 모든 정점의 indegree의 개수를 세준 후 queue에 indegree가 0인 정점을 삽입해 줍니다.

 

정점의 횟수 만큼 반복문을 돌려 다음 작업을 반복합니다.

 

-> 큐의 front를 추출하여 해당 정점에서 나가는 간선을 다 지워준 후 지워진 간선에 의하여 indegree가 0이 되는 정점들을 queue에 삽입해줍니다. (이때 간선을 지워준 다는 것은 간선의 종점인 정점들의 indegree의 개수를 -1 해줌으로 구현 가능합니다.)

 

이 때 큐에 동시에 여러개의 원소가 들어간다면 그 정점들의 순서가 바뀌어도 위상 정렬의 결과에는 영향을 주지 않습니다.

 

 

하지만 우리가 정점의 횟수만큼 반복문을 돌리던 중 큐의 크기가 먼저 0이 되어 버린다면 사이클이 존재하므로 위상 정렬이 불가능하다는 결론이 나옵니다. 사이클에 속하는 정점들이 존재한다면 그 정점들은 모두 indegree가 1이상이라 큐에 들어가지 않기 때문입니다.

 

이러한 방식으로 구현하였을 때 큐에서 추출되는 순서대로 위상정렬이 이루어집니다.

 

 

다음과 같은 그래프의 위상정렬을 해보겠습니다.

 

 

우선 다음과 같이 비어있는 큐를 생성한 뒤 indegree의 개수를 세줍니다.

 

 

 

우선 큐에 indegree가 0인 1번 정점을 삽입해줍니다.

 

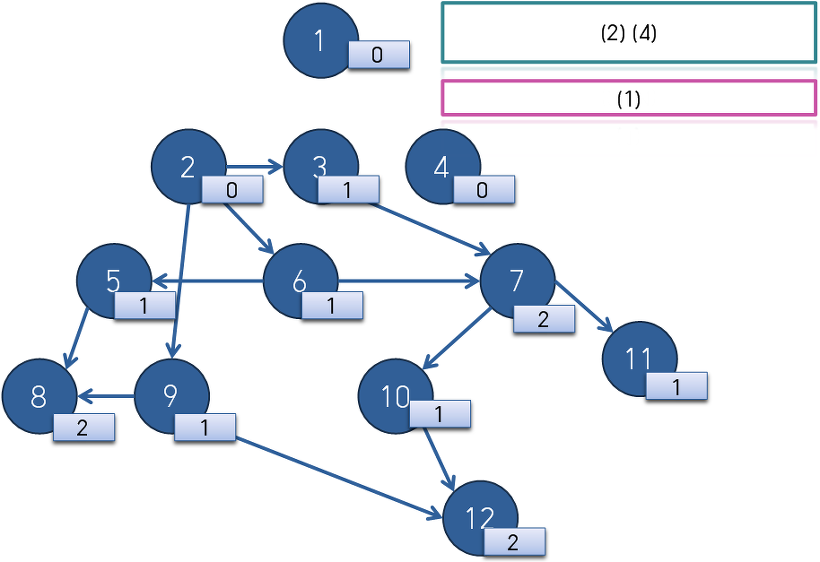
큐의 front인 1번 정점에서 나가는 간선을 모두 지워 준 뒤 indegree가 0이 된 2번 4번 정점을 queue에 삽입합니다.

 

 

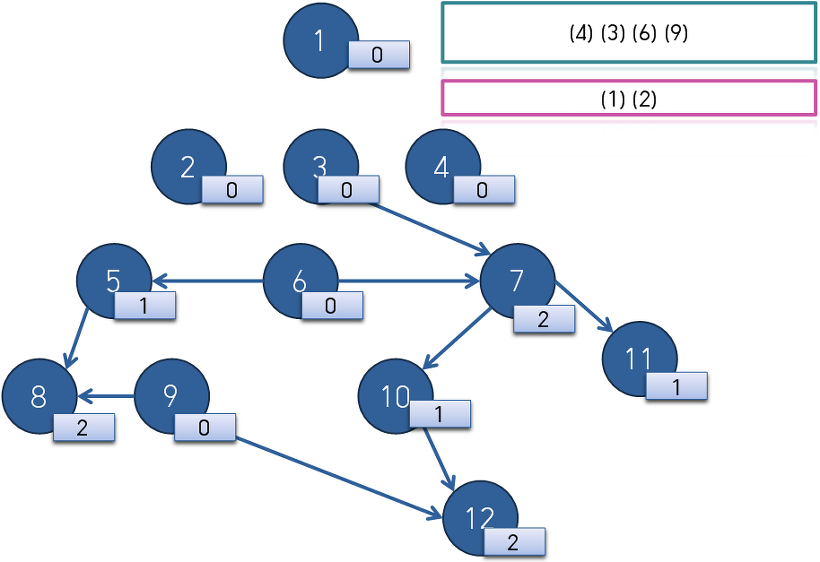
큐의 front인 2번 정점에서 나가는 간선을 모두 지워 준 뒤 indegree가 0이 된 3번 6번 9번 정점을 queue에 삽입합니다.

 

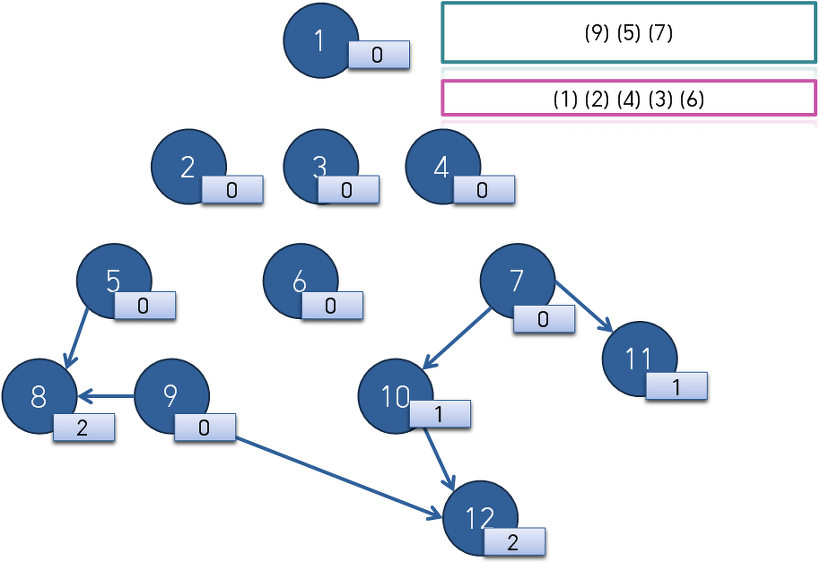
큐의 front인 4번 3번 6번 정점에서 나가는 간선을 순서대로 지워준 후 indegree가 0이 된 5번 7번 정점을 queue에 삽입합니다.

 

큐의 front인 9번 5번 정점에서 나가는 간선을 순서대로 지워준 후 indegree가 0이 된 8번 정점을 queue에 삽입합니다.

 

큐의 front인 7번 8번 정점에서 나가는 간선을 순서대로 지워 준 후 indegree가 0이 된 10번 11번 정점을 queue에 삽입합니다.

 

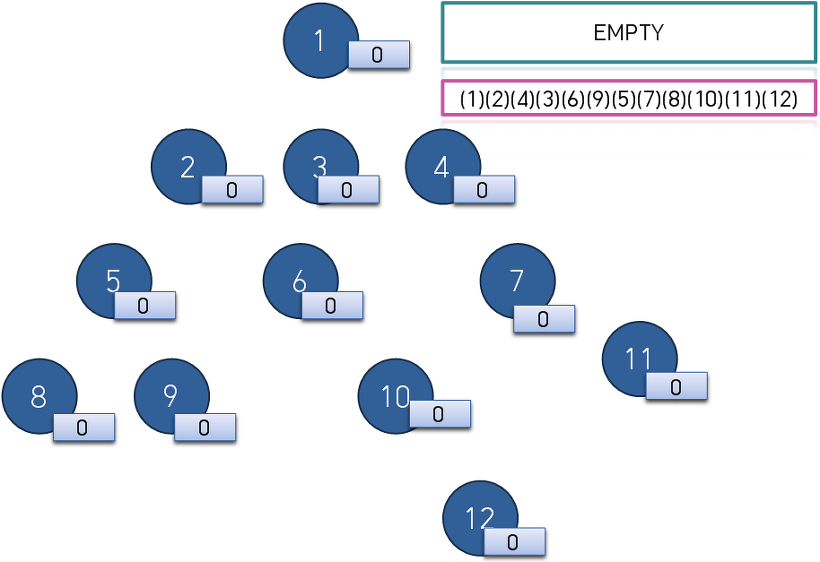
큐의 front인 10번 11번 정점에서 나가는 간선을 순서대로 지워 준 후 indegree가 0이 된 12번 정점을 queue 삽입한 후 12번 정점에서 나가는 간선이 없으니 위상정렬을 종료합니다.

 

위와같이 위상 정렬을 수행했을 때 1->2->4->3->6->9->5->7->8->10->11->12 의 결과를 얻게 됩니다.

출처: https://jason9319.tistory.com/93 [ACM-ICPC 상 탈 사람]

출처: https://jason9319.tistory.com/93 [ACM-ICPC 상 탈 사람]